|
3 讨论
眼的屈光状态取决于眼屈光系统中各屈光因素以及它们之间的协调关系。决定眼屈光力的屈光成分有14种[1],其中主要的是眼轴长度、角膜和晶体的曲率半径、前房深度以及屈光间质的屈光指数等5种。大多数的屈光不正是屈光成分的比例失调,而非异常的光学常数[2]。许多学者应用多种方法探讨影响屈光状态的主要屈光成分的变化规律,为研究屈光不正的性质及形成机制提供理论依据。
3.1 选择研究对象为青少年的依据
我们以青少年(13~25岁)做为研究对象的理由是:(1)尽可能除去发育过程中的变化,(2)排除了老年性改变。
1950年,Slataper[3]在其绘制的人眼屈光
表1 近视屈光度与眼轴长度、玻璃体长度、
晶体厚度、前房深度的关系
| 屈光度(D) |
眼数 |
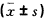 mm mm |
| 眼轴长度 |
玻璃体长度 |
晶体厚度 |
前房深度 |
| -0.25~-1.00
-1.25~-2.00
-2.25~-3.00
-3.25~-4.00
-4.25~-5.00
-5.25~-6.00
-6.25~-7.00
-7.25~-8.00
-8.25~-9.00
-9.25~-10.00
>-10.00 |
26
25
26
29
22
20
19
23
15
14
17 |
23.724±0.61
24.180±0.75
24.990±0.81
25.186±1.02
25.383±1.14
25.678±0.85
25.981±0.75
26.692±0.82
27.688±1.00
28.241±1.27
29.380±1.40 |
16.32±0.52
16.86±0.68
17.46±0.82
18.00±1.02
18.15±0.96
18.39±0.74
18.42±0.71
19.33±0.76
19.98±1.70
20.91±1.08
21.53±1.27 |
3.41±0.31
3.15±0.25
3.30±0.27
3.36±0.43
3.19±0.21
3.35±0.26
3.31±0.19
3.41±0.42
3.56±0.21
3.58±0.49
3.49±0.22 |
3.39±0.33
3.63±0.44
3.63±0.32
3.47±0.54
3.46±0.49
3.36±0.44
3.71±0.30
3.46±0.54
3.55±0.55
3.14±0.42
3.48±0.33 |
统计学分析:
屈光度与眼轴长度与玻璃体长度与晶体厚度与前房深度相关系数r=0.8216r=0.8231r=0.18r=0.047相关系数t检验P<0.001P<0.001P<0.05P>0.05
表2 不同程度近视眼的眼轴长度、晶体厚度、前房深度
| 屈光度(D) |
眼数 |
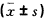 mm mm |
| 眼轴长度 |
晶体厚度 |
前房深度 |
| -0.25~-3.00
-3.25~-6.00
>-6.00
F:
Q检验轻:中
轻:高
中:高 |
78
96
62 |
24.426±0.83
25.656±0.91
27.324±1.10
89.98
P<0.001
P<0.01
P<0.01
P<0.01 |
3.28±0.29
3.31±0.22
3.44±0.32
3.65
P<0.05
P>0.05
P<0.05
P<0.05 |
3.57±0.31
3.42±0.39
3.51±0.46
1.50
P>0.05
P>0.05
P>0.05
P>0.05 |
表3 不同径线角膜屈折力
(n=240)
| 径线 |
最小值(D) |
最大值(D) |
均数(D) |
标准差 |
t检验 |
P值 |
| 水平径线
垂直径线
差值 |
39.625
41.400 |
46.500
47.875 |
43.278
44.516
1.238 |
1.229
1.296
0.900 |
t=17.61 |
<0.001 |
?表4 不同程度近视眼的角膜屈折力
| 屈光度(D) |
眼数 |
水平径线 |
垂直径线 |
| -0.25~-3.00
-3.25~-6.00
>-6.00
F: |
79
98
63 |
43.324±0.853
43.257±0.862
43.262±0.963
0.05
P>0.05 |
44.428±0.867
44.480±0.874
44.630±0.967
0.34
P>0.05 |
表5 近视眼总合散光度与角膜屈折力的关系
| 总合散光度
(D) |
眼数 |
角膜屈折力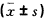 D D |
| 水平径线 |
垂直径线 |
差值 |
| 0
0.25~1.00
1.25~2.00
2.25~3.00
3.25~4.00
4.25~5.00
≥5.25 |
72
55
48
32
17
9
7 |
43.427±1.119
43.456±1.317
42.592±1.164
42.656±1.077
42.667±1.010
42.372±1.121
42.625±0.992 |
44.221±1.050
44.684±1.366
44.381±1.250
45.313±1.125
45.542±1.297
46.632±1.232
47.750±0.725 |
0.793±0.579
1.228±0.559
1.789±0.588
2.656±0.413
3.120±0.673
4.213±0.712
5.125±0.875 |
r=0.9580 P<0.001
表6 各自变量对近视程度影响的逐步回归分析(Sle=0.01)
| 入自变量 |
R2 |
回归系数的显著性检验 |
| step1眼轴长度 |
0.6032 |
P<0.001 |
| step2角膜屈折力 |
0.7496 |
P<0.001 |
演变图提示:人眼从胚胎到成年乃至老年所发生的各种变化中,最主要的是屈光系统的变化。它始终处于一个动态变化过程之中,概括地说,人生有两个远视化阶段,即10岁以前的幼年期和30~60岁的中老年期。仅10~30岁的青少年期是近视化阶段。即使同一个体在近视化阶段屈光各要素的比例关系同两个远视化阶段也是明显不同的。
因此,不分年龄段宠统分析大量人群的样本必然造成数据的偏差,减小数据的可比性。而如果在研究近视眼时将年龄段限制在近视化阶段尽可能去除发育过程中的变化及老年性改变,就能够减小屈光各要素的变异性,增加数据的可比性,以利于分析和发现规律。
3.2 结果分析
3.2.1 眼轴长度与近视程度的相关性
许多学者研究表明[4~6]:近视屈光不正主要表现在眼球前后径增长。本文结果与这一观点相符,即随着近视程度加深,眼轴长度相应增长,二者相关密切。同时我们发现轻度近视眼组轴长的离散度大于中、高度近视眼组,经统计,轻度近视眼组轴性近视占45.25%,高度近视眼组轴性近视占89.89%,与Sugata[7]的报告相一致。表明眼轴增长虽然是近视眼发生的重要原因,但主要与中、高度近视眼相关。至于低度近视眼,如Sorsby[8]指出多是各屈光成分综合作用的结果,而非仅是眼轴延长。
进一步详细分析表明近视每增加1.00DS,眼轴平均增长0.42±0.26mm,Francois计算的数字是1DS约等于0.4mm,均于近年来普遍使用的标准1mm=3.0DS相近。
3.2.2 玻璃体腔长度与近视程度的相关性
玻璃体腔长度与近视程度呈一致性的变化,即随着近视程度的加深而增长,二者相关密切,用回归方程描述二者关系:y(mm)=16.454+0.357x。比较该方程与眼轴和屈光程度的关系方程,可以发现,两方程的斜率(b值)分别为0.357及0.360,非常接近,从而说明眼轴的增长主要是玻璃体腔的增长。
Wiesel[9]从猴眼睑缝合引起的剥夺性近视眼的研究中发现:眼睑闭合引起近视眼组眼球明显扩大,角膜顶点到黄斑区眼轴长度增加21%,而角膜直径和直肌止端到角膜缘的距离无变化,但直肌止端到视神经的距离增加23%。因此,他认为近视眼眼球扩张主要与眼球纵轴增长有关,起初,眼球的增长发生在赤道部,但后来主要发生在赤道以后。该研究论点支持我们的结果。作为近视眼形成的机制,眼轴,特别是玻璃体腔增长的论点得到了支持。
3.2.3 角膜屈折力测量结果分析
(1) 不同程度近视眼角膜屈折力:本组近视眼角膜垂直径线及水平径线屈折力的平均值都明显高于冯葆华[10]报道的我国正常人角膜二径线屈折力(43.513D、43.125D)。但随着近视程度加深,仅垂直径角膜屈折力轻度增大,高度近视组比低度近视组平均增加0.202D,远小于近视增加的度数。推测近视眼角膜屈折力平均较正常人增大,但就眼球总的屈光力而言增大是轻微的,远不如眼轴延长所引起的屈光力增加明显。因而,角膜屈折力的改变主要影响低度近视眼,而对中、高度近视眼,单纯由于角膜屈折力增大而形成的可能性很小。
(2) 不同径线角膜屈折力:本组240只眼角膜垂直径线屈折力几乎全部大于水平径线屈折力,差异有非常显著性。提示青少年时期角膜散光均为循规性散光。
Fulton[11]认为角膜在儿童和青少年时期极少是完全球形的,本组青少年测量的结果支持这一论点,本文角膜散光发生率为99%。由于解剖上的特点,绝大多数垂直径线屈折力大于水平径线屈折力。这种现象引起散光,而散光又导致视网膜成像模糊,启动近视眼的发生。因此Fulton认为,青少年时期任何的屈光不正都应及时并准确地矫正,以确保最好视力,预防近视眼的发生和发展。
(3) 角膜散光与总合散光:本文240只眼总合散光均随着角膜散光度数的增加而增大,二者密切相关。但有一定的离散度,总合散光越小,离散度越大;总合散光越大,离散度越小。72只无总合散光眼仍存在0.25~2.00D的角膜散光,更有甚者,本组中4只眼逆规性散光(0.5~1.5D),而角膜散光却为循规性(0.25~0.75D)。以上充分说明,青少年近视散光主要由角膜散光引起,但除角膜散光的决定性因素外,还有其他的因素影响眼的散光。
Dunne[12,13]研究认为散光的第二因素为晶体散光(lenticular astigmatism),并将角膜散光与总合散光之差称为“剩余散光”(residual astigmatism)。Dunne[14](1996)通过对66例青少年屈光结构的光学测量研究认为:形成散光的屈光成分比较复杂,角膜前、后表面,晶体前、后表面,眼球各光学成分中心的不对称性以及屈光指数的内在变化都是引起散光的因素。其中角膜和晶体前、后表面曲率的不相匹配是主要因素。通过测量可知:由于各径线曲率半径的不同,角膜和晶体前表面产生垂直径线散光,角膜和晶体后表面产生水平径线散光,四者两两相互抵销,未能中和的部分构成眼的散光。因此,他认为一个理想的屈光状态取决于屈光各要素间屈光力的协调平衡。
3.2.4 近视眼成因分析
从效应的多因性出发,本文以屈光程度做为因变量y(dependent variable),以轴长(x1),角膜屈光度(x2),晶体厚度(x3),和前房深度(x4)做为自变量(independent variable),进行逐步回归分析,剔除与因变量无相关的自变量。推导出回归方程:y=-2.025x1-0.983x2+89.907。
该方程提示:眼轴长度对近视程度的影响最为显著,角膜屈折力的影响居其次,其他一些因素的影响相对较小。
结合本文结果讨论可以得知(1)轴性近视为近视眼的主要原因,尤其中、高度近视眼基本是眼轴增长的直接结果。眼轴增长基本是玻璃体腔的增长。(2)在低度近视眼,角膜屈折力的影响似乎比眼轴更大些,轴长多数在正常范围,也可能轻微增大,而角膜屈折力一般较正常眼增大。
上一页 [1] [2] [3] 下一页 |
