1　资料及方法

　　病人源于美国华盛顿大学医院眼科门诊，青光眼病人92例143只眼，其中包括慢性开角型青光眼71例、色素播散性青光眼8例、正常眼压性青光眼13例。所有病人都进行Humphery视野计中心30°检测。正常对照组83例83只眼，随机选一眼作为分析资料，此组源于正常自愿者及人群筛选中的正常者。可疑青光眼组63例104只眼，诊断标准是眼压高于21mmHg或视盘有青光眼样的大视杯，但无视野缺损。表1显示了正常组、可疑青光眼组及青光眼组的平均年龄，经t检验各组年龄无显著性差异。视神经纤维分析仪为NFA　Ⅱ型（产于LDT公司，美国），NFA　Ⅱ型较NFA　Ⅰ型在性能上有很大的提高，特别在测量的可重复性方面有明显的改善。操作NFA遵循以下原则，在明室内，不散瞳，采用自然瞳孔是为了保证扫描激光从瞳孔中央穿过，减少旁侧照射的测量误差。病人头保持正位。每眼扫描三次，将三次扫描结果的平均值作为基准图像。

　　青光眼组主要根据眼底视盘及视野指数-平均缺损（mean　defects，MD）的情况分为三期，早期青光眼：C／D≤0．7，MD＜10dB；中期青光眼：C／D＝0．8～0．9，MD＜25dB；晚期青光眼：C／D＞0．9。表1显示了各期青光眼的平均年龄、MD。与以往有关的研究不同，我们分析的参数不仅仅源于厂家提供的参数，有些参数是提取原始数据计算的，原始数据存放在region．txt文件中，它包括两类数据，即积分值及平均值。由于积分值受测量环直径的影响，测量环越大，其测量面积越大，积分值亦越大，因此视盘的大小会影响测量值。而平均值不受此值的影响。所以我们选择平均值作为分析的基本数据。测量的数据采集于视盘周围的1.8个视盘半径处的圆环，此环的宽度为10微米，每10°计算一个平均值，一周有36个原始数据。这些数据转换到SPSS统计软件进行分析。

　　本研究有三类参数，1、2类参数由仪器本身提供。（1）总值参数，即各象限总和值，分为上、下、鼻、颞象限。（2）比值参数，即上或下象限与鼻象限的比值，早期研究发现正常人的偏振延迟值有较大的变异，通过除去鼻象限（基准值）减少变异，青光眼晚期才发生鼻象限的损害，故以此作基准。（3）调制参数，由原始数据计算求出。首先求基线，基线的定义是鼻侧及颞侧最低点的平均值。上象限调制峰值＝上象限的最高点－基线；上象限调制总值＝上象限总值－基线下总值。此类参数由我们提出，理由是青光眼早期损害部位在视盘的上下极，此处正是偏振延迟曲线的双峰。

　　统计分析采用SPSS软件的多因素逐步判别分析法。

　　2　结果

　　表1列出了各组的年龄分布及视野的情况，各组的年龄经t检验无显著性差异。

　　为了分析青光眼RNFL偏振延迟曲线的特征，图1绘制了正常组及各期青光眼组的平均偏振延迟曲线，由上至下的四条曲线分别是正常组、早期、中期及晚期青光眼组的平均延迟曲线。很明显其曲线的基线（波谷）在各组变化不明显，双峰依青光眼程度的加重而降低。

表1　各组的年龄及视野缺损的情况

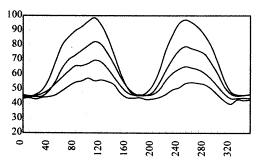
图1　正常组及各期青光眼的NFA测量的平均延迟曲线

　　为了便于与以往的研究进行比较，表2列出了以往类似研究青光眼分组的标准及各参数的情况，以往研究都采用了组间偏振延迟平均差比值的概念。此平均差比值＝（正常组延迟平均值－青光眼组延迟平均值）／正常组延迟平均值，此比值越大说明该参数组间差异大、越敏感。

表2　各研究中青光眼分组的标准

　　及总值参数的平均差比值

　　图2显示早期、中期青光眼与正常眼组间的平均延迟差比值，图中可见调制参数的平均差比值明显高于总值参数及比值参数的平均差比值。

早期青光眼

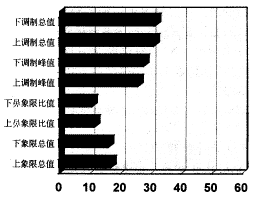
中期青光眼

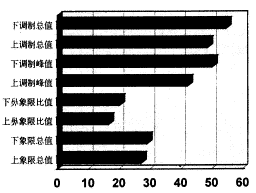
图2　早期、中期青光眼组与正常组

　　之间偏振延迟的平均差比值

　　为了反映各组各类参数偏振延迟值的分布情况，图3、图4用框格图显示了各组数据的分布情况及组间的差异。图3是总值参数及比值参数的分布框格（框格内含有75％的数据），正常组与早期青光眼组之间有较大的重叠。图4是调制参数的分布框格，正常组与早期青光眼组之间基本分离。

　　表3是各参数以正常组、早期青光眼分组时用多因素逐步判别分析法计算的Wilks值及F值，Wilks值是组内总和的平方与所有值总和平方的比值，当两个观察组一致时，此值为1。当组内变异小，组间差异大时，此值接近0。所以小的Wilks值说明各组的均值差异明显。从表3可看出调制峰值、调制总值的Wilks值均较NFA提供参数（总值参数、比值参数）的Wilks值小。

上一页  [1] [2] [3] 下一页